Loops

Fibonacci Sequence

$F_1 = 1$, $F_2 = 1$ and $F_i = F_{i-1} + F_{i-2}$, $i = 3, 4, ...$

n=20;
F(1)=1;
F(2)=1;
for i=3:n
    F(i)=F(i-1)+F(i-2);
end
F

F =

 Columns 1 through 11:

      1      1      2      3      5      8     13     21     34     55     89

 Columns 12 through 20:

    144    233    377    610    987   1597   2584   4181   6765

clear all
F(1)=1;
F(2)=1;
n=3;
F(3) = F(1) + F(2);
while n<=10
    F(n)=F(n-1)+F(n-2);
    n=n+1;
end
F

F =

    1    1    2    3    5    8   13   21   34   55

A simple while loop

x=1
while x<=10
    x=2*x
end

x =  1
x =  2
x =  4
x =  8
x =  16

A=[1 2 3; 4 5 6; 7 8 9];
B=[5 6 7;8 9 0;3 4 5];
disp('sum of two matrices without loop')
A+B
for i=1:3
    for j=1:3
        C(i,j)=A(i,j)+B(i,j);
    end
end
disp('sum of two matrices using for loop')
C

sum of two matrices without loop
ans =

    6    8   10
   12   14    6
   10   12   14

sum of two matrices using for loop
C =

    6    8   10
   12   14    6
   10   12   14

Matrix multiplication

A=[1 2 3; 4 5 6; 7 8 9];
B= [3 2 1; 6 5 4; 9 8 7];
C=zeros(3);
disp('Matrix multiplication without loop')
disp(A*B)
for i=1:3
    for j=1:3
       % C(i,j)=0;
        for k=1:3
            C(i,j)=C(i,j)+A(i,k)*B(k,j);
        end
    end
end
disp('Matrix multiplication using for loop')
disp(C)

Matrix multiplication without loop
    42    36    30
    96    81    66
   150   126   102
Matrix multiplication using for loop
    42    36    30
    96    81    66
   150   126   102

Find factorial $n! = 1. 2. 3. ... (n-1)n$

n=5;
f=1;
i = 1;
for i=1:n
    f=f*i;
    i=i+1;
end
disp('using for loop')
disp(f)

f1=1;
i=1;
while i<=n
    f1=f1*i;
    i=i+1;
end
disp('using while loop')
disp(f1)

using for loop
 120
using while loop
 120

function f = fact(n)
    f = prod(1:n);
endfunction

fact(5)

ans =  120

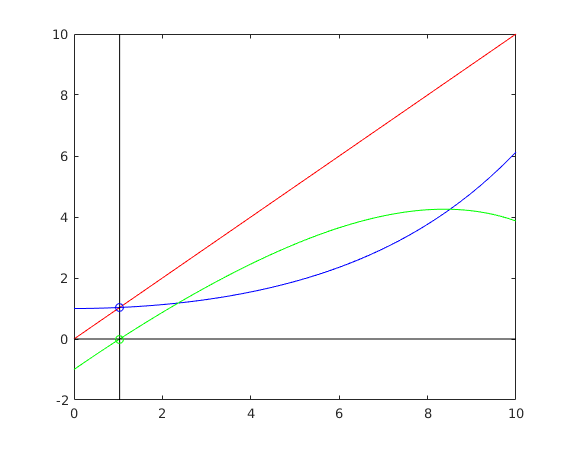
Fixed point iteration, $x = \phi(x)$, $x_n =\phi(x_{n-1})$. For example $x = cosh(x/4)$

clear all
disp('Fixed point iteration');
phi = @(x) cosh(x/4);
xf=1;
er = 1;
k=0;
while ((er > 1e-8) && (k < 100))
    xnew = phi(xf);
    er = abs(xnew-xf);
    xf = xnew;
    k = k+1;
end
xf
k

Fixed point iteration
xf =  1.0336
k =  7

%plot gnuplot
f = @(x) x - phi(x);
x=0:0.05:10;
y1=x;
y2=phi(x);
plot(x,y1,'r',x,y2,'b')
hold on 
plot(x,f(x),'g',x,0*x,'k',xf*ones(length(-2:0.05:10),1),-2:0.05:10,'k')
plot(xf,xf,'ob',xf,0,'og')
hold off

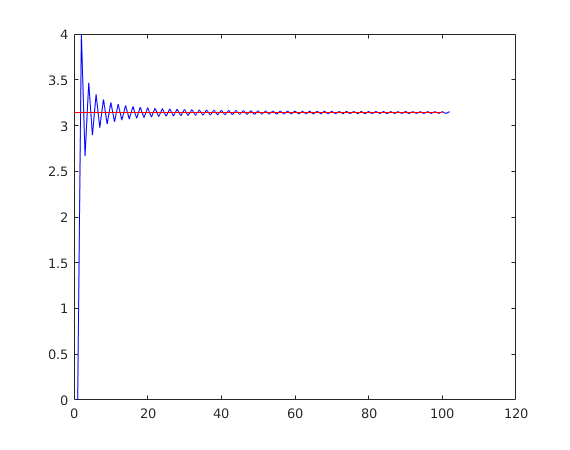
Leibniz formula for $\pi$,

$\frac{\pi}{4} = \sum_{n=0}^{\infty} \frac{(-1)^n}{2n+1}$

clear piapprox
n=100;
piq=0;
piapprox = 0;
for i=0:n
    piq=piq+((-1)^i)/(2*i+1);
    piapprox = [piapprox, piq*4];
end
piapprox(end)
%plot gnuplot
plot(piapprox,'b')
hold on
plot(0:n,pi*ones(length(0:n),1),'r')
hold off

ans =  3.1515