%plot gnuplot

$f'(x_0) \approx \frac{f(x_0 + h) -f(x_0)}{h} + O(h)$

error = $|f'(x_0) - \frac{f(x_0 + h) -f(x_0)}{h}| \approx O(h)$

clear all
format long
f = @(x) sin(x);
x0=1.2;
f0=sin(x0);
fp=cos(x0);
i=-6:0.5:0;
h=10.^i;
err=abs(fp-(sin(x0+h)-f0)./h);
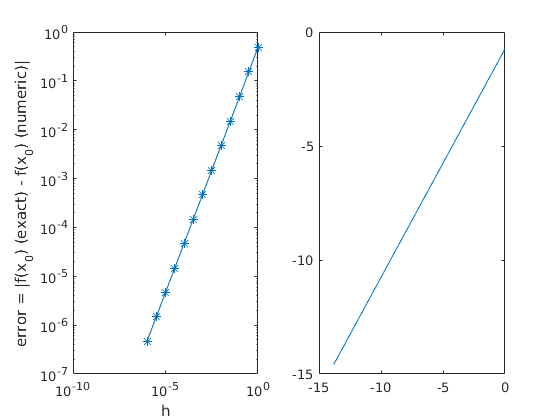
subplot(1,2,1)
loglog(h,err,'-*');
xlabel('h')
ylabel('error = |f(x_0) (exact) - f(x_0) (numeric)|')
c1 = polyfit(log(h),log(abs(err)),1)
hold on
subplot(1,2,2)

plot(log(h), c1(1)*log(h)+c1(2))

c1 =

   1.002263431950136  -0.740850628132612

c1(1) = 1.002263431950136 means the order of error is $\approx 1$.

f = @(x) sin(x);
x0 = 0:0.001:20;
f0 = f(x0);
J = length(f0);
dx=x0(2)-x0(1);
slope = [(f0(2:J)-f0(1:J-1))/dx, (f0(J)-f0(J-1))/dx]; % Forward
x1 = 0:0.5:20;
figure;
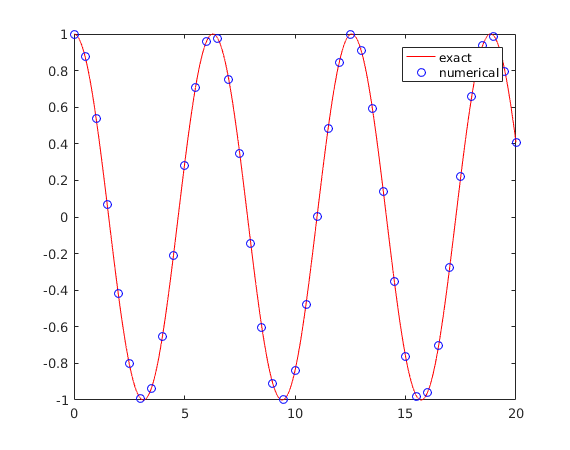
plot(x0,slope,'r',x1,cos(x1),'ob')
legend('exact','numerical')

Try yourself

Find second derivative, $f''(x_0) \approx \frac{f(x_0 + h) -2 f(x_0) +f(x_0 - h)}{h^2} + O(h^2)$.
Verify the order of error.