The roots of quadratic equations $a x^2 + b x + c = 0$ are $ r = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$.

In [21]:
a=1; b=0; c=-3;
d=b^2-4*a*c;
if d>=0
    disp('roots are positive.');
end

roots are positive.
In [22]:
a=1; b=1; c=3;
d=b^2-4*a*c;
if d>=0
    disp('roots are positive.');
else
    disp('roots are immaginary');
end

roots are immaginary
In [23]:
a=1; b=1; c=3;
d=b^2-4*a*c;
if d>0
    disp('roots are positive and distinct');
    r1 = (-b+sqrt(d))/(2*a)
    r2 = (-b-sqrt(d))/(2*a)
elseif d==0
    disp('roots are real and same');
    r = -b/(2*a);
else
    disp('roots are immaginary');
    re = -b/(2*a); im = sqrt(-d)/(2*a);
    printf ("r1 = %f + i %f \n",re, im);
    printf ("r2 = %f - i %f \n",re, im);
end

roots are immaginary
r1 = -0.500000 + i 1.658312 
r2 = -0.500000 - i 1.658312
In [24]:
%plot gnuplot
In [25]:
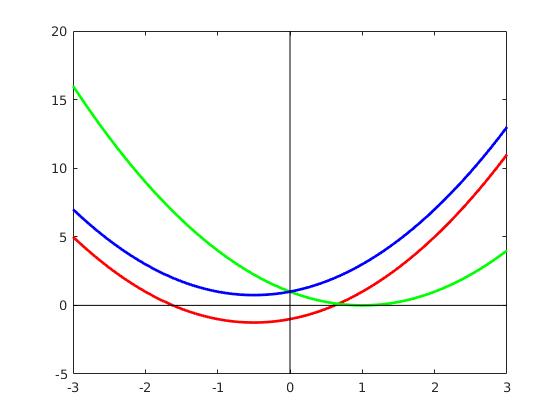
% define a quadretic function with a, b and c parameters
f = @(x, a, b, c) a*x.^2 + b*x + c;

x= -3:0.1:3;
y1=f(x,1,1,-1); %we get two real roots 
y2=f(x,1,-2,1); %one real root
y3=f(x,1,1,1); %no real root

plot(x,y1,'r',x,y2,'g',x,y3,'b')
hold on
plot(x,0*x,'k',0*ones(length(x),1),10*x,'k') %plotting axises
hold off
axis([-3, 3, -5,20])

Quadretic functions